This vignette is intended to get you up and running using ‘postpack’ to process your MCMC output by showcasing some of the main features.
Prequisites
‘postpack’ requires that your MCMC samples are stored in
mcmc.list objects (class and methods supplied by the ‘coda’
package). MCMC samples should be produced from at least two chains –
single chain output has not been tested with ‘postpack’ functions. Some
MCMC interfaces produce this output by default, while others require an
extra step to convert to mcmc.list.
JAGS
mcmc.list output is returned by:
rjags::coda.samples()jagsUI::jags.basic()- The
$sampleselement ofjagsUI::jags()
NIMBLE
To obtain mcmc.list output, users should set the
samplesAsCodaMCMC = TRUE argument when calling
nimble::runMCMC().
Stan
The output of rstan::stan() can be converted to
mcmc.list format using
rstan::As.mcmc.list().
WinBUGS/OpenBUGS
The output of both:
can be converted to mcmc.list format using
coda::as.mcmc.list() or
postpack::post_convert().
If your samples were generated another way (e.g., a custom MCMC
algorithm or a package like ‘MCMCpack’), check out
?postpack::post_convert to see how you may be able to
reformat them.
Getting Started
This vignette uses an example mcmc.list object called
cjs to illustrate the main features of ‘postpack’, see
?cjs or vignette("example-mcmclists") for more
details. To follow along, load it and ‘postpack’ into your session:
Query MCMC Attributes
You can return the dimensions of the MCMC run using:
post_dim(cjs)
## burn post_burn thin chains saved params
## 11000 50000 200 2 500 21These elements should be self-explanatory, but see
?post_dim for details. You can extract one of these
dimensional elements quickly by specifying the types
argument, e.g., notice that there are 21 saved nodes by running
post_dim(cjs, types = "params").
The parameter names of these nodes will be crucial in subsetting
them, so you should be able to check them out quickly at any time. This
is the purpose of the get_params() function:
get_params(cjs)
## [1] "B0" "sig_B0" "B1" "sig_B1" "b0" "b1" "SIG" "p"This shows you the base node names that were monitored during model
fitting. If you wish to see the element indices associated with each
node as well, supply the type = "base_index" argument:
get_params(cjs, type = "base_index")
## [1] "B0" "sig_B0" "B1" "sig_B1" "b0[1]" "b0[2]"
## [7] "b0[3]" "b0[4]" "b0[5]" "b1[1]" "b1[2]" "b1[3]"
## [13] "b1[4]" "b1[5]" "SIG[1,1]" "SIG[2,1]" "SIG[1,2]" "SIG[2,2]"
## [19] "p[2]" "p[3]" "p[4]"Extracting Posterior Summaries
A cornerstone of ‘postpack’ is the post_summ() function,
which is for extracting posterior summaries for particular nodes of
interest.
## sig_B0 sig_B1
## mean 0.8440230 0.243479572
## sd 0.6187583 0.262166509
## 50% 0.6820298 0.178356796
## 2.5% 0.2766108 0.005735707
## 97.5% 2.4394721 0.820640886The output is in a simple, easily subsettable matrix format (unlike
coda::summary.mcmc()), which makes plotting these summaries
more straight-forward. Presented by default are posterior mean, standard
deviation, and the 50%, 2.5%, and 97.5% quantiles. You can report other
quantiles using probs if desired and round them using
digits:
## sig_B0 sig_B1
## mean 0.844 0.243
## sd 0.619 0.262
## 2.5% 0.277 0.006
## 25% 0.490 0.081
## 50% 0.682 0.178
## 75% 1.035 0.319
## 97.5% 2.439 0.821One of the key features is that the params argument
selects nodes based on regular expressions, so all elements of the
"b0" node can be summarized with:
post_summ(cjs, "b0")
## b0[1] b0[2] b0[3] b0[4] b0[5]
## mean 1.3753033 2.3192679 1.751486 1.5200421 1.0824184
## sd 0.2067011 0.3564031 0.238889 0.2032504 0.2077227
## 50% 1.3674581 2.2779459 1.728931 1.5075479 1.0754654
## 2.5% 0.9614656 1.7836702 1.324638 1.1597562 0.6748646
## 97.5% 1.8053107 3.1633955 2.287703 1.9605019 1.5194312Several ‘postpack’ functions accept the params argument
(always in the second argument if it is present) to specify queries from
the mcmc.list passed to post, so learning to
use it is key. More information on using regular expressions to extract
particular nodes can be found in
vignette("pattern-matching").
Estimates of the uncertainty associated with MCMC sampling in the
mean and quantiles can be obtained using the mcse argument
(which calls mcmcse::mcse() and
mcmcse::mcse.q()):
post_summ(cjs, "^B", mcse = TRUE)
## B0 B1
## mean 1.59031238 0.415103100
## sd 0.49113008 0.212836348
## 50% 1.56878458 0.397436350
## 2.5% 0.55133227 0.061825217
## 97.5% 2.58753866 0.863829917
## mcse_mean 0.01359695 0.011192343
## mcse_50% 0.01724213 0.009013355
## mcse_2.5% 0.18139264 0.025923187
## mcse_97.5% 0.06398231 0.042813775Summaries for each chain can be obtained using the
by_chain = TRUE argument:
post_summ(cjs, "^B", by_chain = TRUE)
## , , chain1
##
## B0 B1
## mean 1.5571300 0.4180811
## sd 0.4614706 0.2401460
## 50% 1.5502780 0.3988950
## 2.5% 0.5012706 0.0608274
## 97.5% 2.5107643 0.8543241
##
## , , chain2
##
## B0 B1
## mean 1.6234948 0.41212506
## sd 0.5178997 0.18191380
## 50% 1.5922041 0.39674020
## 2.5% 0.5687639 0.07524337
## 97.5% 2.6084912 0.87875912Extracting MCMC Diagnostics
‘postpack’ features two primary ways of diagnosing the
convergence/adequate sample behavior of MCMC chains: numerically and
visually. Both methods use the params argument to allow
users to have control over which nodes get diagnostics.
post_summ() includes two additional arguments for
obtaining numerical diagnostics:
## sig_B0 sig_B1
## mean 0.8440230 2.434796e-01
## sd 0.6187583 2.621665e-01
## 50% 0.6820298 1.783568e-01
## 2.5% 0.2766108 5.735707e-03
## 97.5% 2.4394721 8.206409e-01
## Rhat 1.0220000 1.043000e+00
## neff 500.0000000 4.320000e+02neff = TRUE triggers a call to
coda::effectiveSize() to estimate the number of MCMC
samples that are independent and Rhat = TRUE triggers a
call to coda::gelman.diag() to calculate the commonly used
Rhat convergence diagnostic (numbers near 1 are ideal, greater than 1.1
may be problematic). "Rhat" will always be rounded to three
digits, and "neff" will always be rounded to an integer,
regardless of the value of the digits argument.
Viewing the density and trace plot for a parameter is another common
way to evaluate algorithm convergence. The diag_plots()
function serves this purpose (which, unlike
coda:::plot.mcmc(), allows plotting the densities color
coded by chain and only for specific nodes):
diag_plots(cjs, params = "SIG")
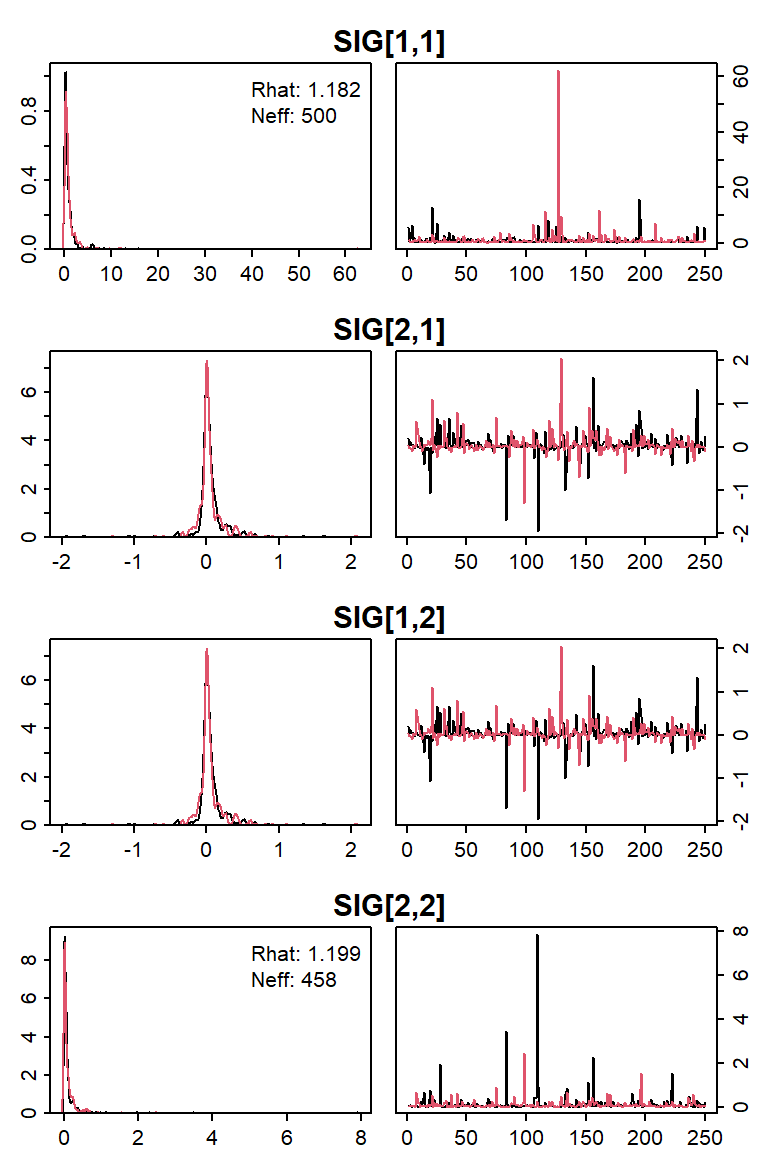
Options exist to:
- Display the Rhat and effective MCMC samples for each node (the
show_diagsargument, which accepts value of"always","never", or"if_poor_Rhat"with the last one being the default. See?diag_plotsfor details). - Plot the output in a new external device (the
ext_deviceargument). - Change the size of the graphics device (the
dimsargument). - Change the layout of parameters on the device (the
layoutargument). - Save the output to a PDF graphics device (the
saveargument, which then requires that you enter thefileargument, which is the file name of the PDF complete with the".pdf"extension). - Thin the chains by some percentage (at quasi-evenly spaced
intervals) before drawing the trace plot – this can help manage the file
size when generating many plots with many samples while still providing
much of the same inference as the unthinned output. The argument
keep_percent = 0.8is passed topost_thin(), and would discard 20% of the samples prior to trace plotting. This thinning does not affect the density plot visual – all retained samples are plotted there.
The dims and layout arguments are set to
"auto" by default – for adjustment of these settings, see
?diag_plots.
The more chains there are in the mcmc.list object passed
to the post argument, the more colors will be
displayed.
Extracting Posterior Samples
Often you will want to take a subset out of your output while retaining each saved posterior sample, for example, to plot a histogram of the samples or to calculate the posterior of some derived quantity as though it had been included as part of the model code.
b0_samps = post_subset(cjs, "b0")
By default, the output will be a mcmc.list which allows
it to play nicely with the rest of the ‘postpack’ functions (e.g.,
get_params(b0_samps)). However, performing plotting or
calculation tasks on posterior samples might be easier if they were
combined across chains and stored as a matrix (nodes as columns, rows as
samples):
b0_samps = post_subset(cjs, "b0", matrix = TRUE)
Note that if you wish to retain the chain and iteration number of
each posterior sample when converting to a matrix with
post_subset(), you can pass the optional logical arguments
chains and iters (both are FALSE
by default).
head(post_subset(cjs, "b0", matrix = TRUE, chains = TRUE, iters = TRUE))
## CHAIN ITER b0[1] b0[2] b0[3] b0[4] b0[5]
## [1,] 1 11200 1.275155 2.632859 1.860819 1.708103 0.8804635
## [2,] 1 11400 1.308511 2.077802 1.518087 1.198710 0.9843441
## [3,] 1 11600 1.338846 2.473211 1.358235 1.156759 0.8060235
## [4,] 1 11800 1.654078 2.703028 1.498338 1.279799 1.0339362
## [5,] 1 12000 1.118555 2.313318 1.819527 1.189711 0.9702624
## [6,] 1 12200 1.188926 2.653793 1.633183 1.539144 0.8438322In some cases, it may be easier to keep all nodes
except those matched by params. For this
this, you can use post_remove() (if
ask = TRUE, you will be prompted to verify that you wish to
remove the nodes that were matched – this is the default):
# check out param names get_params(cjs)
## [1] "B0" "sig_B0" "B1" "sig_B1" "b0" "b1" "SIG" "p"# remove all SIG nodes cjs2 = post_remove(cjs, "SIG", ask = FALSE) # did it work? get_params(cjs2)
## [1] "B0" "sig_B0" "B1" "sig_B1" "b0" "b1" "p"Matrix/Array Nodes
array_format()
Notice that the "SIG" node is a matrix (there are two
dimensions of element indices in the node names):
(SIG_ests = post_summ(cjs, "SIG", digits = 2))
## SIG[1,1] SIG[2,1] SIG[1,2] SIG[2,2]
## mean 1.09 0.05 0.05 0.13
## sd 3.19 0.26 0.26 0.45
## 50% 0.47 0.02 0.02 0.03
## 2.5% 0.08 -0.33 -0.33 0.00
## 97.5% 5.95 0.58 0.58 0.67You may want to create a matrix that stores the posterior means (or
any other summary statistic) in the same format as they would be found
in the model. For this, you can use array_format():
array_format(SIG_ests["mean",])
## [,1] [,2]
## [1,] 1.09 0.05
## [2,] 0.05 0.13Although this is a basic example, this function becomes more useful for higher dimensional nodes – dimensions between 2 and 10 are currently supported.
array_format() requires a vector of named elements,
where the element names contain the correct indices to place them in
(e.g., "SIG[1,1]" and "SIG[2,2]"). Based on
the indices in the element names, array_format() determines
the dimensions of the object in the model and places the elements in the
correct location.
array_format() will respect missing values. As an
example, suppose the the model did not specify what
"SIG[2,1]" should be. In this case, it will not be returned
as a tracked node element in the mcmc.list (at least in
JAGS). We can simulate this behavior by removing that node from the
output, and seeing that array_format() inserts an
NA in the proper location:
cjs2 = post_remove(cjs, "SIG[2,1]", ask = FALSE) array_format(post_summ(cjs2, "SIG")["mean",])
## [,1] [,2]
## [1,] 1.094471 0.04547222
## [2,] NA 0.12787612
vcov_decomp()
The "SIG" node represents a variance-covariance matrix
in the model. Sometimes it is desirable to decompose this matrix into a
vector of standard deviations and a correlation matrix. Rather than
perform this calculation on the posterior summary of "SIG",
we can perform it for each posterior sample to obtain a posterior of the
correlation matrix. This is the purpose of
vcov_decomp():
SIG_decomp = vcov_decomp(cjs, param = "SIG")
## Decomposing variance-covariance matrix node: SIG (2x2)
##
## Note the characteristics of the output obtained:
class(SIG_decomp)
## [1] "mcmc.list"## burn post_burn thin chains saved params
## TRUE TRUE TRUE TRUE TRUE FALSEget_params(SIG_decomp, type = "base_index")
## [1] "sigma[1]" "sigma[2]" "rho[1,1]" "rho[2,1]" "rho[1,2]" "rho[2,2]"The nodes "sigma[1]" and "sigma[2]"
represent the square root of the diagonal elements
"SIG[1,1]" and "SIG[2,2]" (and are thus the
same as the "sig_B0" and "sig_B1" nodes stored
in cjs), and the "rho" elements represent to
correlation matrix – and posterior samples exist now for each. The names
used for these newly-created nodes can be changed using the
sigma_base_name and rho_base_name
arguments.
You can now build the posterior median correlation matrix:
array_format(post_summ(SIG_decomp, "rho")["50%",])
## [,1] [,2]
## [1,] 1.0000000 0.2685727
## [2,] 0.2685727 1.0000000When using vcov_decomp(), you are recommended to always
keep check = TRUE, which will ensure that the samples are
from a valid variance-covariance matrix prior to performing the
calculation. Setting invert = TRUE will take the inverse of
the matrix from each posterior sample prior to performing the
calculations (e.g., if you had monitored a precision matrix rather than
a covariance matrix).
Manipulate Samples
post_thin()
If your downstream analyses of the posterior samples require many
calculations, then it may be advantageous to develop the code with a
smaller but otherwise identical version of the posterior output before
unleashing them on the full output. You can thin the chains at
quasi-evenly spaced intervals using post_thin():
post_thin(cjs, keep_percent = 0.25)
Which would retain 25% of the samples from each chain, and return the
result as an mcmc.list object. You may instead use the
keep_iters argument to specify the number of iterations you
wish to keep per chain.
post_bind()
It may be desirable to combine posterior samples from the same MCMC run together in a single object. This case may arise when calculating derived quantities, and for organizational purposes you want to have them in one object as opposed to two. The two objects must have the same number of chains and saved iterations, and should be calculated from the same model run.
Two mcmc.lists
The derived quantities stored in SIG_decomp from above
are stored as an mcmc.list object and were calculated from
the same model using consistent rules, so have the same dimensions. This
makes it easy to use:
cjs = post_bind(post1 = cjs, post2 = SIG_decomp)
and note that you have the new calculated nodes in you main object:
get_params(cjs)
## [1] "B0" "sig_B0" "B1" "sig_B1" "b0" "b1" "SIG" "p"
## [9] "sigma" "rho"You can now quickly verify that "sig_B0" and
"sig_B1" are the same as "sigma[1]" and
"sigma[2]", respectively:
post_summ(cjs, "sig")
## sig_B0 sig_B1 sigma[1] sigma[2]
## mean 0.8440230 0.243479572 0.8440230 0.243479572
## sd 0.6187583 0.262166509 0.6187583 0.262166509
## 50% 0.6820298 0.178356796 0.6820298 0.178356796
## 2.5% 0.2766108 0.005735707 0.2766108 0.005735707
## 97.5% 2.4394721 0.820640886 2.4394721 0.820640886
One mcmc.list and one matrix
Suppose instead that your derived quantities are stored as a matrix:
iterations along the rows and quantities along the columns. Binding this
to an mcmc.list object involves:
1.) Obtaining the matrix of the derived quantity(ies),
2.) Deciding on a name for each of your quantities, and
3.) Binding the derived list to the main list.
For step (1), generate such a matrix of derived quantities now,
representing the inverse logit transformation of each of the
"b0" elements:
# extract the raw samples from cjs in matrix form b0_samps = post_subset(cjs, "b0", matrix = TRUE) # perform a derived quantity calculation eb0_samps = exp(b0_samps)/(1 + exp(b0_samps))
Now you have a derived quantity, so for step (2) change the names that each quantity will be stored as:
Finally, for step (3) combine the samples using
post_bind():
cjs = post_bind(post1 = cjs, post2 = eb0_samps)
If the two objects contain duplicate node names, the values from the
object passed to the post2 argument of
post_bind() will have the suffix supplied under the
argument dup_id ("_p2" by default), and a
warning will be returned.